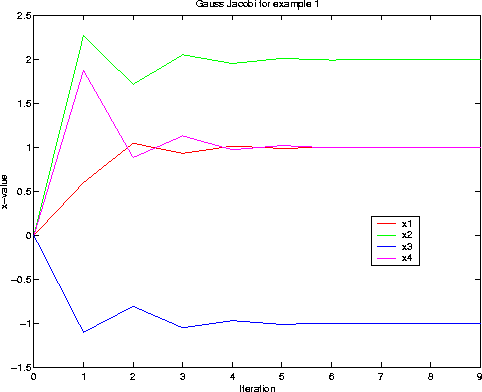
The actual numbers are in the book, table 7.1
The same problem with the Gauss Seidel Algorithm:
Here are the Results for the x(i), and a tolerance of 0.001:

The actual numbers are in the book, table 7.1
The same problem with the Gauss Seidel Algorithm:
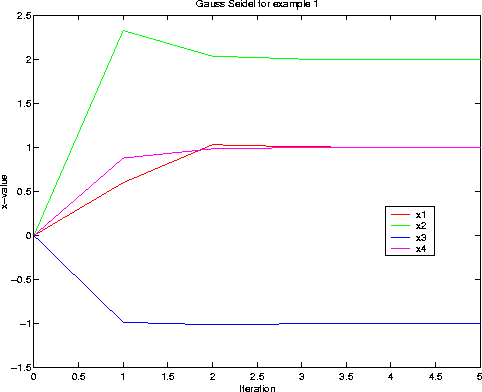
Again, the actual numbers are in the book, table 7.2