The Matlab code used is here
Typical output in the the file output.log can be found here
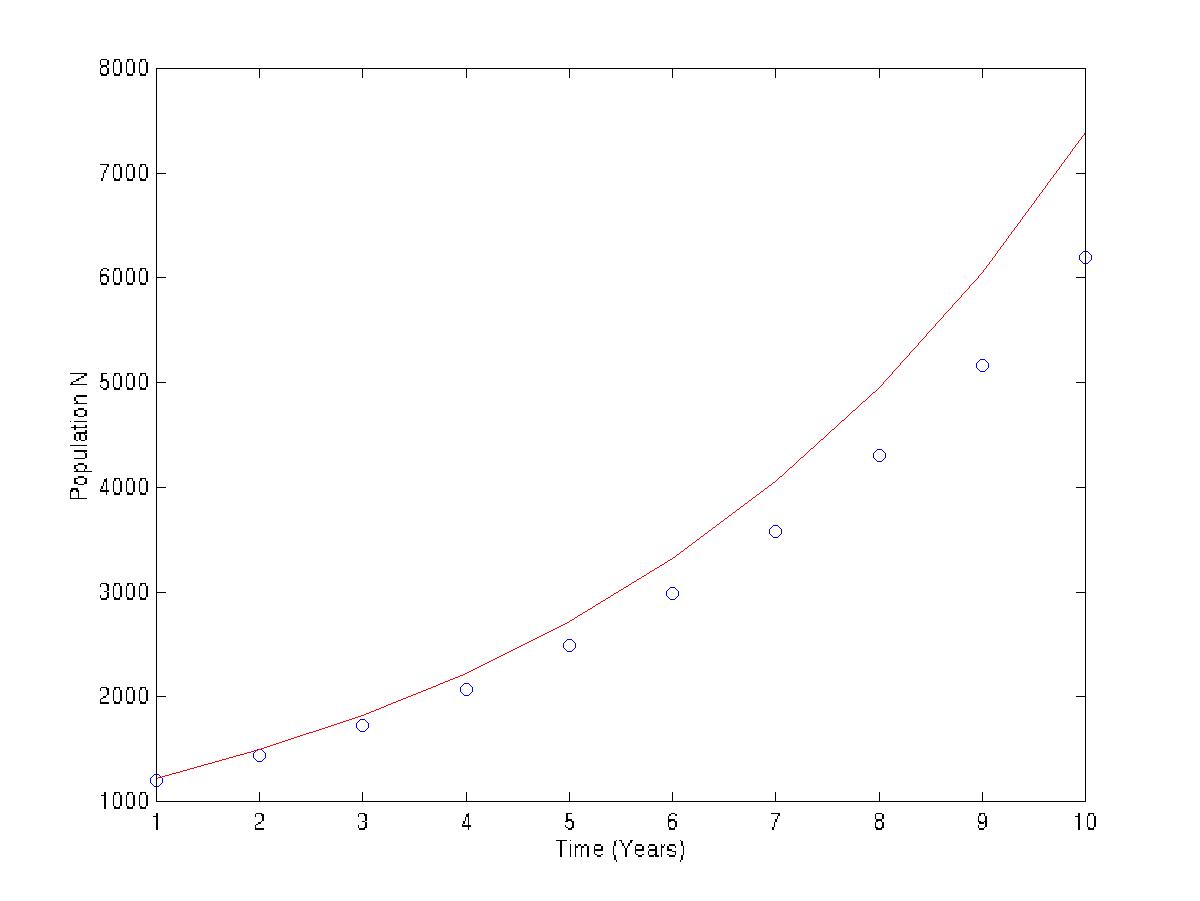
h=1.0

h=0.1
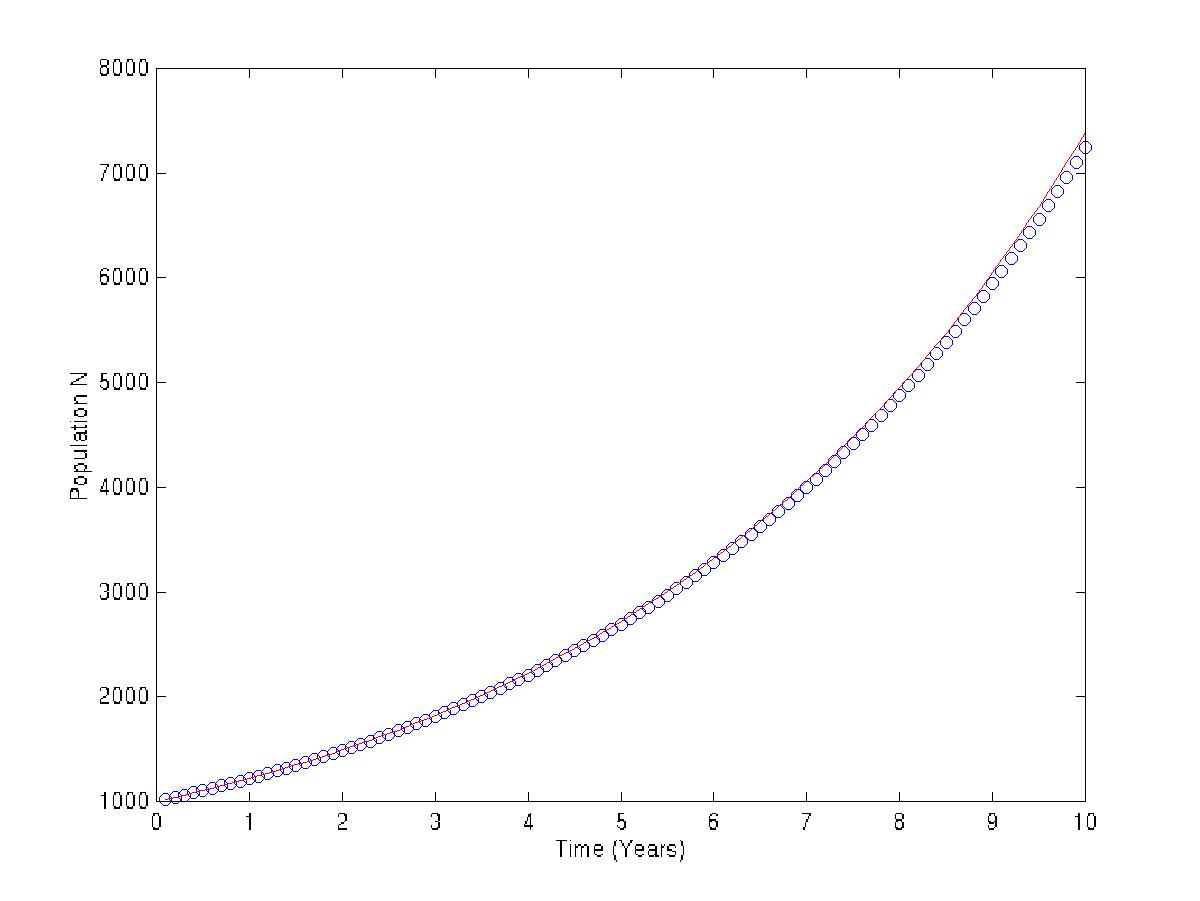
h=0.05
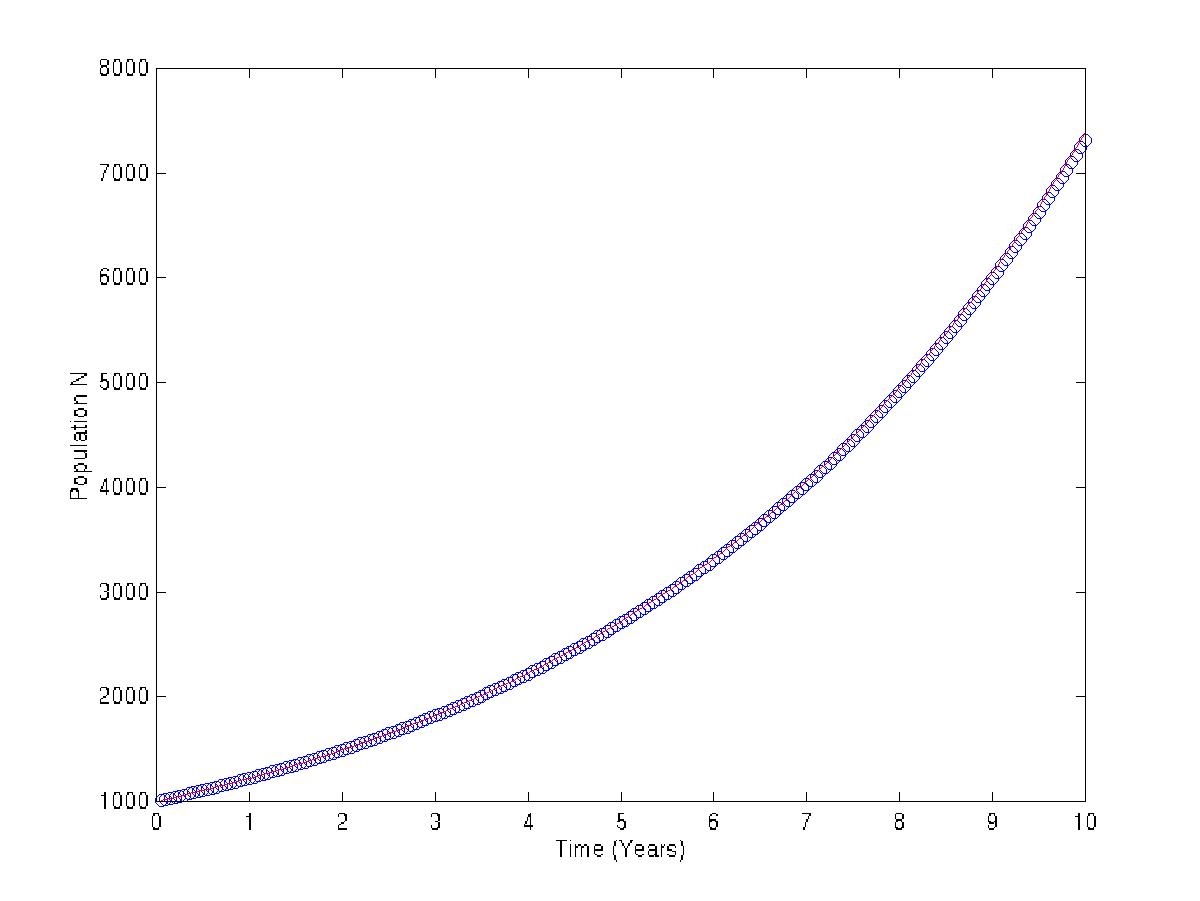
h=0.0.25
| h | Numerical Result | Exact Result | Error |
| 1.0 | 6.1917364e+03 | 7.3890561e+03 | 1.1973197e+03 |
| 0.1 | 7.2446461e+03 | 7.3890561e+03 | 1.4440998e+02 |
| 0.05 | 7.3160179e+03 | 7.3890561e+03 | 7.3038247e+01 |
| 0.025 | 7.3523251e+03 | 7.3890561e+03 | 3.6730991e+01 |
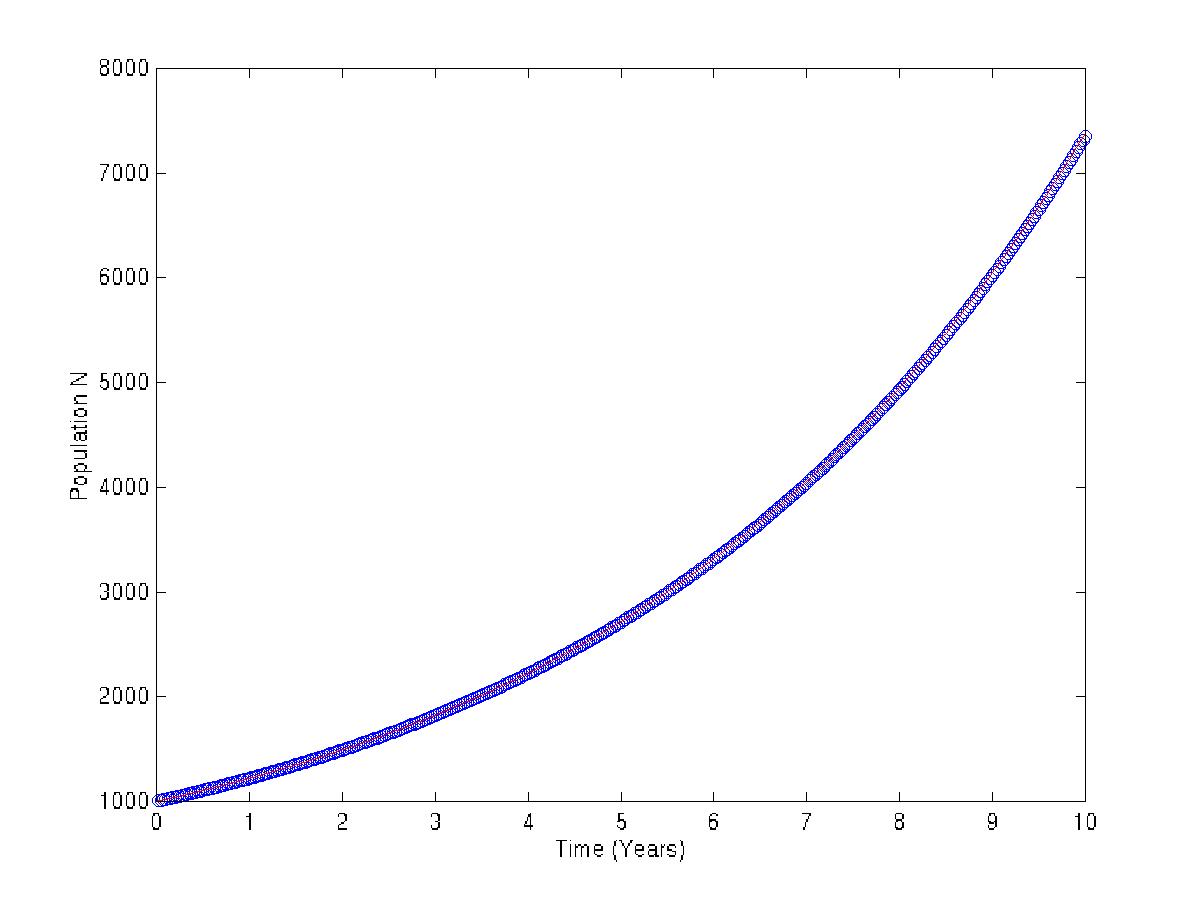
| 0.001 | 7.3889083e+03 | 7.3890561e+03 | 1.4777774e-01 |
For a really small timestep, the error actually increases due when the timestep is decreased (Theorem 5.10 in the textbook). For example, with the above code, and tmax=0.0000001, we get:
| h | Numerical Result | Exact Result | Error |
| 0.00000002 | 1.0000000e+03 | 1.0000000e+03 | 5.6843419e-13 |
| 0.00000001 | 1.0000000e+03 | 1.0000000e+03 | 1.1368684e-13 |
| 0.000000005 | 1.0000000e+03 | 1.0000000e+03 | 2.1600499e-12 |
| 0.000000001 | 1.0000000e+03 | 1.0000000e+03 | 4.4337867e-12 |