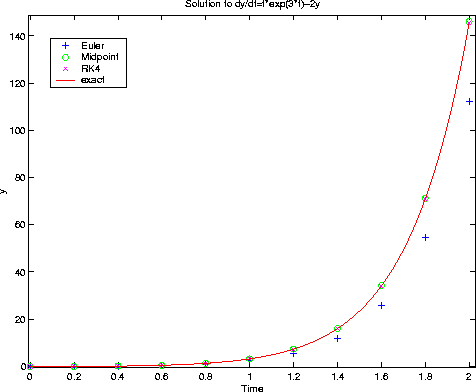
Let's check the results of the 3 different methods for h=0.2.

Clearly, Midpoint Method and Runge-Kutta method are much better than Euler's method.
Let's zoom in on the last point:
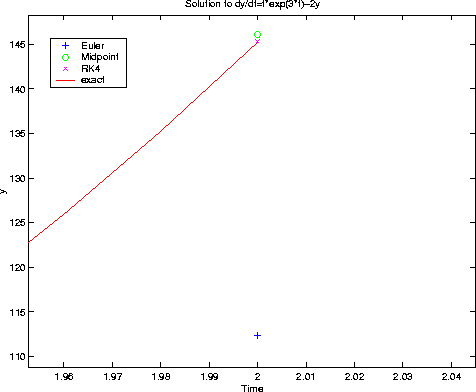
Now we can see that the Runge Kutta Method performs better than the midpoint method, as expected.
Let's look at some numbers to make this point; we compare the numbers at t=2.0:
| h | Exact Result | Euler Result | Midpoint Result | RK4 Result | Euler Error | Midpoint Error | RK4 Error |
| 0.2 | 1.4523510e+02 | 1.1235584e+02 | 1.4608271e+02 | 1.4533231e+02 | 3.2879261e+01 | 8.4760818e-01 | 9.7209396e-02 |
| 0.1 | 1.4523510e+02 | 1.2872794e+02 | 1.4552122e+02 | 1.4524124e+02 | 1.6507158e+01 | 2.8611680e-01 | 6.1465615e-03 |
| 0.05 | 1.4523510e+02 | 1.3698635e+02 | 1.4531508e+02 | 1.4523548e+02 | 8.2487460e+00 | 7.9977337e-02 | 3.8346926e-04 |